Tabla de contenidos
- Introducción
- Incrustación de Entrada (Input Embedding)
- Codificación Posicional (Positional Encoding PE)
- El Codificador
- El Decodificador
- Capa Lineal y Capa Softmax
- Entrenamiento del Transformador
- Conclusión
Introducción
El Transformador es actualmente una de las arquitecturas más populares para el Procesamiento del Lenguaje Natural (NLP). Periódicamente, podemos escuchar noticias sobre nuevas arquitecturas y modelos basados en transformadores que generan mucho interés y expectativas en la comunidad.
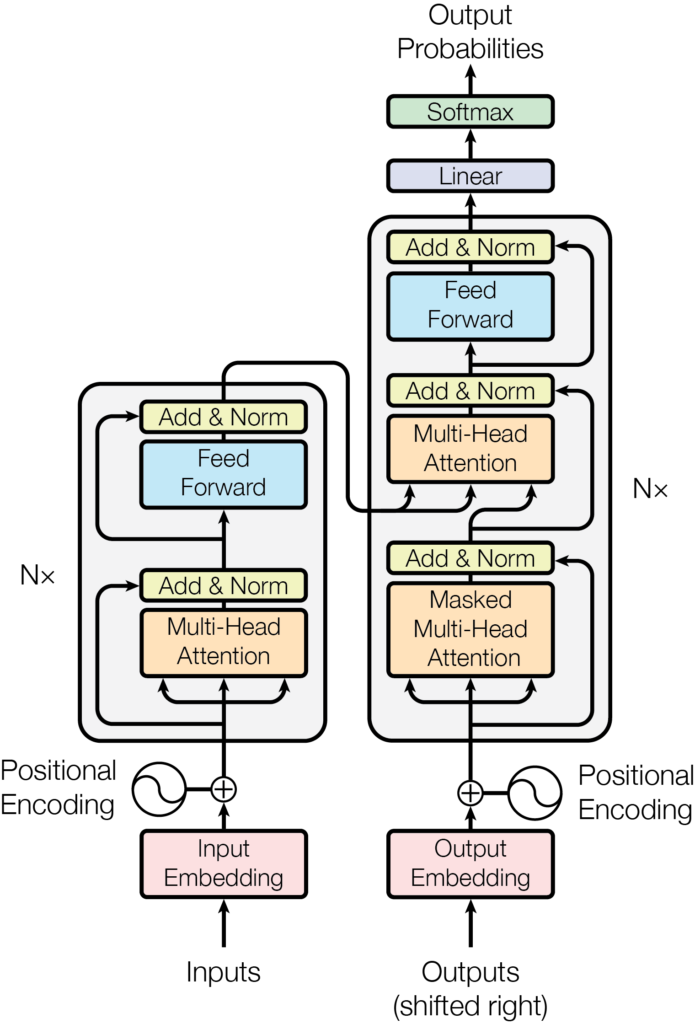
Fuente: Attention is all you need
Google Research y miembros de Google Brain propusieron inicialmente el Transformador en el artículo de 2017 Attention is all you need. Aunque podemos descargarlo y leerlo, sus conceptos aún están restringidos a los iniciados en la elegante nomenclatura matemática.
El Transformador superó a otras arquitecturas existentes basadas en LSTM y RNN, obteniendo mejores resultados en las evaluaciones y un entrenamiento más rápido. El mecanismo de atención del Transformador es una operación de «palabra a palabra» que encuentra cómo cada palabra se relaciona con las demás en la secuencia, incluida la misma palabra. En el presente documento, explicaré la arquitectura y el funcionamiento interno de un Transformador de la manera más simple posible.
Incrustación de Entrada (Input Embedding)

Comenzando desde el principio, la arquitectura del Transformador inicia con la subcapa de Incrustación de Entrada (Input Embedding), que convierte la secuencia de entrada en vectores de dimensión d_{model}=512.
🎓 El valor de d_{model}=512 fue establecido por los diseñadores de la arquitectura para establecer una dimensión constante a la salida de cada subcapa del modelo. El valor de esta dimensión puede ser modificada dependiendo de los objetivos.
Un tokenizador transforma el flujo de entrada en tokens normalizando el texto a minúsculas y dividiéndolo en subpartes; además, proporcionará una representación vectorial de enteros (basada en un vocabulario existente) que se utilizará para el proceso de incrustación (embedding). Por ejemplo:
Input = "Roses are red and violets are blue"
Tokens = ["roses", "are", "red", "and", "violets", "are", "blue"]
Tokenized = [8271, 1029, 3674, 9273, 2384, 1029, 9873]
A continuación, la subcapa de incrustación recibe el vector tokenizado. Para cada palabra, esta subcapa debe producir un vector de tamaño d_{model}=512. Por ejemplo, para las palabras «rojo» y «azul», que son colores, los vectores de incrustación de palabras deberían ser similares::
blue=[ 0.36138474, -0.16811648, -0.03733656, -0.58750702, -0.81279167,
-0.86249844, 0.69673459, -0.79213212, 0.9278906 , 0.42308278,
-0.12308109, 0.2383174 , 0.44863208, 0.98666162, -0.12830655,
-0.56420363, 0.69459217, 0.72405279, 0.92023563, -0.84536481,
0.86299045, -0.88166481, -0.9087216 , 0.99420482, -0.73118714,
...
-0.47495972, -0.94366021, -0.97624231, -0.9792538 , 0.20736778,
0.1248088 , 0.6344501 , -0.54432975, -0.35632176, -0.6670839 ,
-0.48141856, -0.3503394 , -0.94319604, 0.48421567, -0.12854877,
-0.48260166, -0.845398 , 0.67561689, 0.29778234, 0.03009221,
0.25067641, -0.81864996, -0.51513235, -0.44608639, -0.65686229]
🎓 La similitud del coseno se puede utilizar para verificar si dos vectores de incrustación (embeddings) son similares. Para obtener más información sobre la teoría: Similitud del Coseno en Scikit-Learn.
Los vectores de incrustación proporcionan mucha información al Transformador acerca de cómo las palabras en una secuencia están relacionadas. Sin embargo, aún se necesita información para indicar la posición de las palabras en una secuencia, y para esto se utiliza el proceso de Codificación Posicional.
Codificación Positional (Positional Encoding PE)
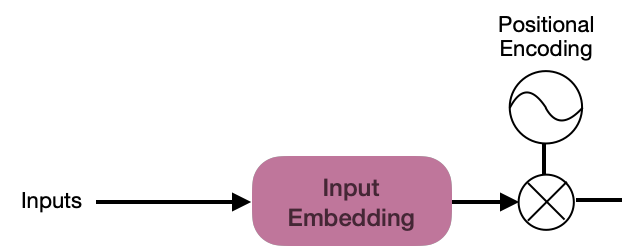
Cada palabra en la secuencia inicial debe tener información de PE, pero la generación de este vector debe ser simple, ya que el enfoque principal del Transformador es el mecanismo de atención.
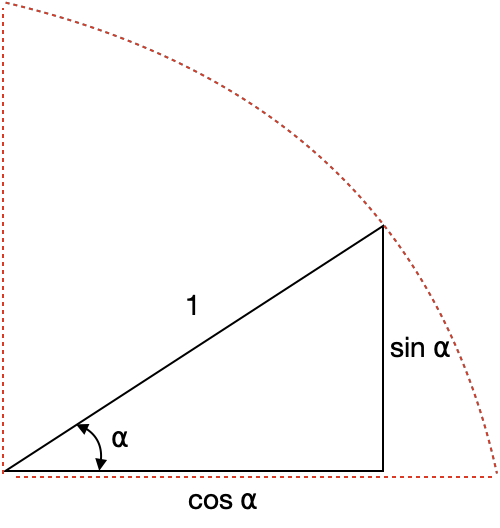
El desafío en esta tarea es generar un vector de dimensión d_{model}=512 para cada vector de salida de la función PE. Los autores de la arquitectura utilizaron ingeniosamente una esfera unitaria para representar la PE con valores de seno y coseno.
🎓 Con la idea de la esfera unitaria, los autores propusieron funciones seno y coseno que pueden generar diferentes valores de PE para cada dimensión i de las 512 establecidas en el vector de incrustación de palabras (word embedding).
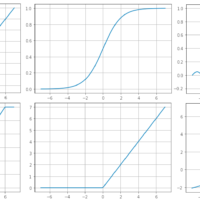
PE_{(pos\:2i)}=sin \left (\frac{pos}{10000^{\frac{2i}{d_{model}}}} \right)(Plot sin in Google)
PE_{(pos\:2i+1)}=cos \left (\frac{pos}{10000^{\frac{2i}{d_{model}}}} \right) (Plot cos in Google)
El proceso aplicará la función seno a los números pares i\: \in \left [ 0,\:255\right ] y la función coseno a los números impares i\: \in \left [ 256,\:512\right ]. Los valores de PE (Posición Codificada) se codifican dentro de la esfera unitaria y permiten una representación sencilla de la posición de los elementos en la secuencia.
El siguiente ejemplo es una traducción en Python del concepto de Codificación Posicional, evaluado para la posición 3:
import math
d_model = 512
def positional_encoding(position):
pe = [None] * d_model
for i in range(0, 512, 2):
pe[i] = math.sin(position / (10000 ** ((2 * i) / d_model)))
pe[i + 1] = math.cos(position / (10000 ** ((2 * i) / d_model)))
return pe
print(positional_encoding(3))
Por ejemplo, supongamos que tenemos la oración «The sky is blue,» la matriz de Codificación Posicional PE será:
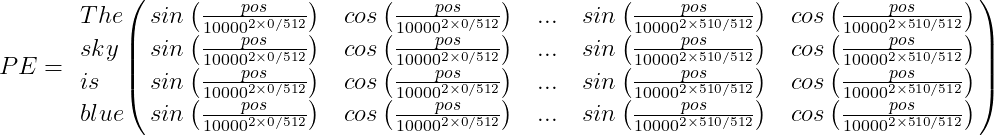
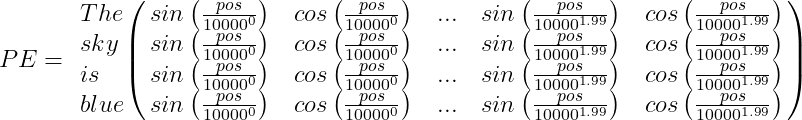
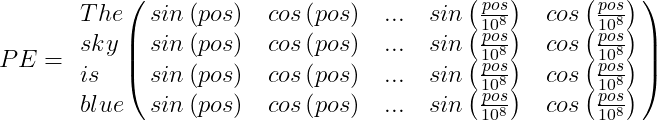
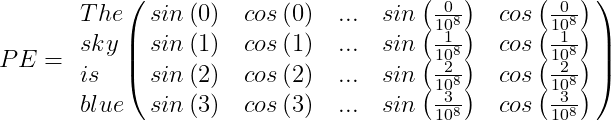
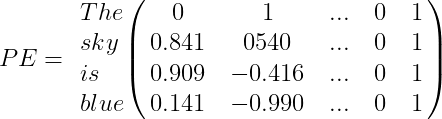
Finalmente, el vector de codificación de palabras debe sumarse al vector de codificación posicional, y el bloque codificador/decodificador será alimentado con el resultado:
Embedding_{output} = Embedding_{initial}+PE_{word\:position}
Sin embargo, los valores de incrustación de palabras a veces son demasiado pequeños y podrían ser prácticamente desconsiderados. En este caso, la solución es escalar los valores, por ejemplo, utilizando la media del PE.
El codificador
En su visión más simple, el Transformador es una arquitectura de codificador-decodificador, donde el codificador aprende la representación de Codificación Posicional del texto de entrada y la envía al decodificador. El decodificador recibe lo que ha sido aprendido por el codificador y genera una salida.
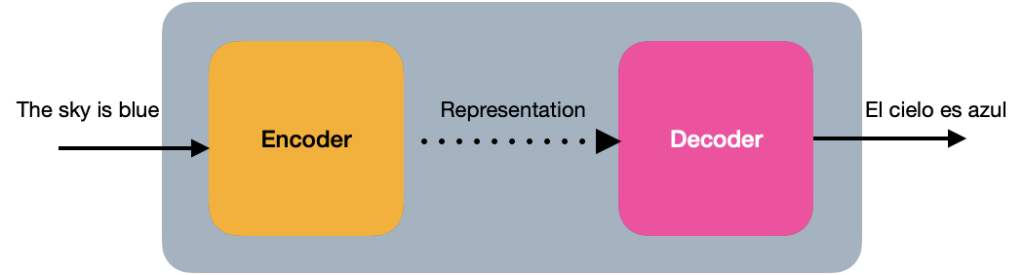
Internamente, en más detalle, el Transformador consiste en una pila de N codificadores, cada uno enviando su salida al siguiente. El último codificador devuelve la representación de la secuencia de entrada. Para la explicación, a partir de ahora, utilizaremos un valor de N=2.
🎓 Los autores originales del Transformador asignaron el valor de N=6 en «Attention is all you need».
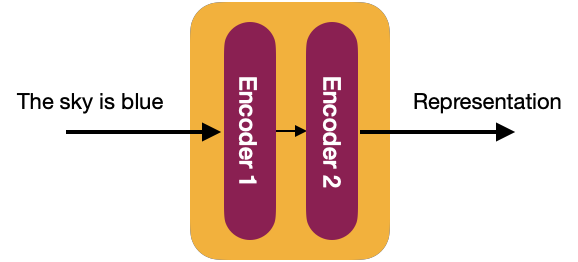
Cada bloque decodificador está compuesto de 2 subcapas:
- Atención multicabezal
- Red Prealimentada
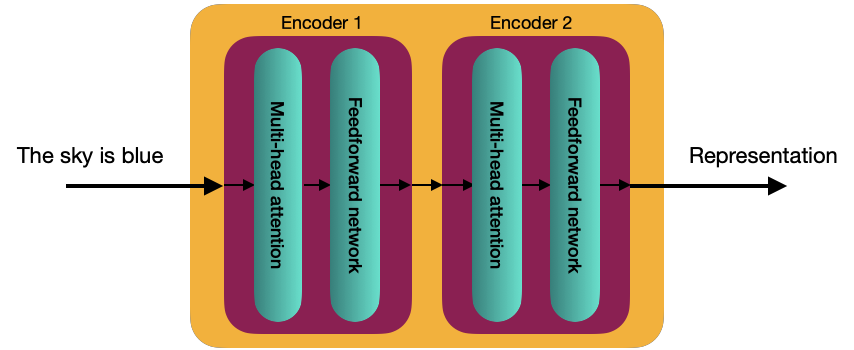
Antes de empezar a explicar esos dos componentes, es necesario entender el mecanismo de auto-atención.
Mecanismo de Auto-atención
Considera la siguiente oración:
John and Paul wrote several songs when they were inspired.
En esta oración, el mecanismo de auto-atención calcula la representación de cada palabra, y la relación con las otras palabras en la oración proporciona más información acerca de la palabra. Por ejemplo, el término «they» debería estar relacionado con «John» y «Paul» y no con «songs».

Un ejemplo más sencillo para comprender cómo funciona el mecanismo de auto-atención es la oración «The sky is blue». Los codificadores reciben vectores de incrustación de palabras de dimensión d_{model}=512 de cada palabra de la oración, por ejemplo:
x_1=\begin{bmatrix} 3.23 & 0.65 & ... & 4.78 \end{bmatrix} ==> «The»
x_2=\begin{bmatrix} 1.26 & 6.35 & ... & 7.99 \end{bmatrix} ==> «sky»
x_3=\begin{bmatrix} 9.25 & 1.68 & ... & 4.26 \end{bmatrix} ==> «is»
x_4=\begin{bmatrix} 6.84 & 2.98 & ... & 11.48 \end{bmatrix} ==> «blue»
Con estos vectores, podemos ensamblar la matriz de incrustación X, con d=[4 \times 512]:

Crearemos tres matrices adicionales a partir de esta matriz X que sirve como el «mecanismo de auto-atención»:
- Q, matriz de consulta
- K, matriz de clave
- V, matriz de valor
Para crear estos arreglos, necesitamos además tres nuevas matrices de pesos. La dimensión utilizada en el artículo original era d_k=64; por lo tanto, los vectores de peso tendrían una dimensión de d_{model} \times d_k\Rightarrow 512 \times 64, que se inicializan con valores aleatorios:
- W^Q, matriz de pesos de consulta
- W^K, matriz de pesos de clave
- W^V, matriz de pesos de valor
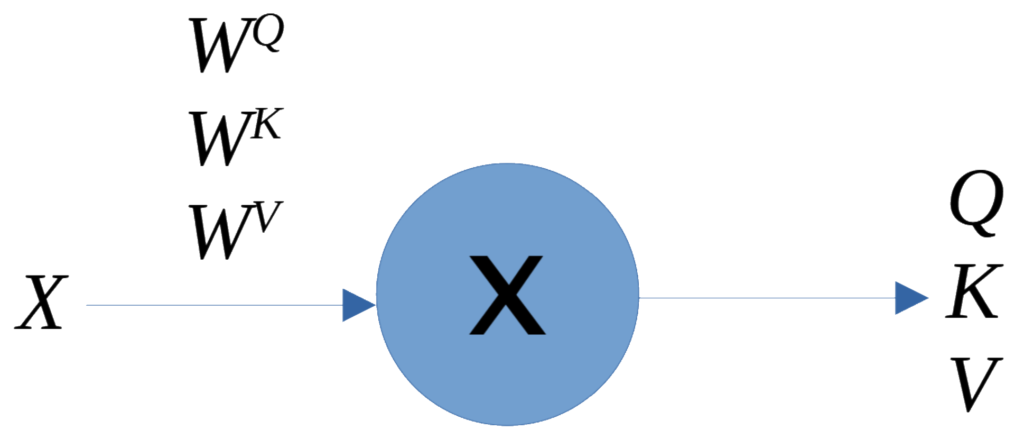
Las matrices de pesos contienen los valores óptimos aprendidos durante el entrenamiento, por lo que cada matriz Q, K, y V, es el producto de la matriz de incrustación (embedding) X con la matriz de pesos correspondiente, lo que genera matrices de 4 \times 64:
- Q = X \times W^Q
- K = X \times W^K
- V = X \times W^V

Cada una de las cuatro filas en cada matriz representa cada palabra de la oración inicial, «The sky is blue.»
Proceso del Mecanismo de Auto-atención
1. Computar el producto punto Q \cdot K^T
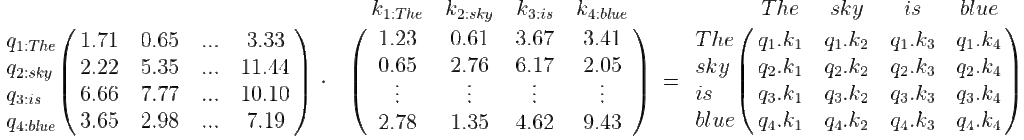
Los elementos del arreglo resultante indican la relación entre las palabras. Por ejemplo,q_1.k_1 es la relación de la palabra «The» consigo misma y tiene un valor alto, pero q_1.k_3 es la relación entre «The» y «is» y tiene un valor bajo. La relación entre «sky» y «blue» (q_2.k_4) tendrá un valor un poco más alto porque hay una relación entre el sustantivo y el adjetivo. Por ejemplo:
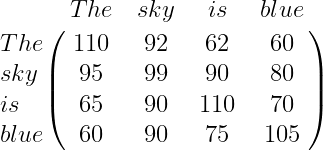
De esta manera, podemos decir que calcular el producto escalar entre la matriz de consulta, Q, y la matriz de clave, K^T, esencialmente nos da el valor de similitud, que nos ayuda a entender cuán similar es cada palabra en la oración a todas las demás palabras.
2. Computar QK^T/\sqrt{d_k}. Esta acción es útil para obtener gradientes estables, donde d_k=64 es la dimensión del vector clave.
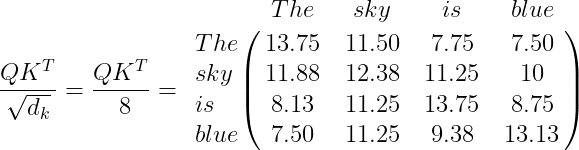
Los valores de la matriz resultante deben ser normalizados, y si utilizamos la función Softmax\left ( \frac{QK^T}{\sqrt d_k} \right ) (ver Softmax), podemos formalizar los valores en un rango de 0 a 1.
import numpy as np
def softmax(x):
max = np.max(x,axis=1,keepdims=True)
e_x = np.exp(x - max)
sum = np.sum(e_x,axis=1,keepdims=True)
f_x = e_x / sum
return f_x
V = np.array([[13.75, 11.50, 7.75, 7.50],
[11.88, 12.38, 11.25, 10],
[8.13, 11.25, 13.75, 8.75],
[7.5, 11.25, 9.38, 13.13]])
softmax(V)
array([[0.90105641, 0.09497065, 0.0022335 , 0.00173945],
[0.29994872, 0.49453184, 0.15975023, 0.04576921],
[0.00331791, 0.07513861, 0.91537572, 0.00616775],
[0.00304195, 0.12934693, 0.01993542, 0.8476757 ]])
La suma de los valores en cada fila es igual a 1. Con estos valores, podemos entender cómo cada palabra en la oración se relaciona con todas las demás palabras. Esto se llama la matriz de puntuación (score matrix).
3. Luego, es necesario calcular la matriz de atención Z:
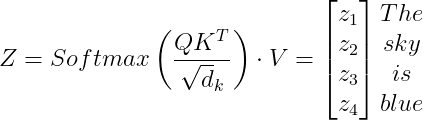

Z=\begin{bmatrix} 4.18336201 & 0.65278898 & ... & 4.22437426 \\ 5.94802206 & 3.00072113 & ... & 4.4028484 \\ 3.09529998 & 1.49925765 & ... & 9.9459073 \\ 4.76015677 & 2.69495094 & ... & 2.17709763 \end{bmatrix}
La matriz de atención Z es una matriz de, en el ejemplo de la oración, 4 filas y 512 columnas. Cada fila corresponde al vector de auto-atención de la palabra correspondiente.
El mecanismo de auto-atención se llama atención de producto punto escalado ya que calculamos el producto punto entre los vectores Q y K y escalamos los valores por (\sqrt {d_k}).
Mecanismo de atención multicabezal
Para el Transformador, vamos a calcular varias matrices de atención. ¿Pero por qué necesitamos varias matrices? Esto nos ayuda en contextos idiomáticos donde el significado de una palabra es ambiguo, por ejemplo:
Tom was crying because he was blue.
Un único mecanismo de atención decidiría que Tom estaba llorando porque su color es azul (blue), siendo dominado por la palabra «Tom». Y si en la mayoría de las oraciones en las que «blue» implica que es un color, al tener solo una «cabeza de atención», el mecanismo aprenderá correctamente que es un color. Sin embargo, al tener «múltiples cabezas de atención», es más probable que uno de esos mecanismos de atención aprenda de las oraciones en las que se implica que «azul» es un estado de ánimo, y al concatenar los resultados de las «múltiples cabezas de atención», la matriz de atención será más precisa.
¿Cómo podemos computar matrices de atención múltiple? Sugongamos que vamos a computar dos matrices de atención: Z_1 y Z_2.
Para computar Z_1 primero, creamos las tres matrices Q_1, K_1, y V_1, lo que implica multiplicar la matriz de incrustación y las tres matrices de peso W_{1}^{Q}, W_{1}^{K}, y W_{1}^{V}. Ahora, la matriz de atención se computa de la siguiente manera:
Z_1=Softmax\left ( \frac{Q_1K_{1}^{T}}{\sqrt{d_k}} \right ) \cdot V_1
De la misma manera para Z_2
Z_2=Softmax\left ( \frac{Q_2K_{2}^{T}}{\sqrt{d_k}} \right ) \cdot V_2
De esta manera, podemos calcular cualquier cantidad de matrices de atención. Supongamos que necesitamos ocho matrices de atención (el valor en «La atención lo es todo»). En ese caso, podemos concatenar todas las cabezas de atención y multiplicar el resultado por una nueva matriz de pesos W_0 entrenada para representar los valores óptimos para el mecanismo de atención.
Multi-head \: attention=Concatenate\left ( Z_1, Z_2, Z_3, Z_4, Z_5, Z_6, Z_7, Z_8 \right ) \cdot W_0
Red Prealimentada
La red prealimentada consiste en solo dos capas densas con activación ReLU. Los mismos parámetros se aplican en diferentes partes de la oración, pero es distinto a los bloques del codificador.
Un componente adicional para conectar la entrada y los bloques del codificador es el componente de suma y normalización, que es una conexión seguida de la normalización de capa.
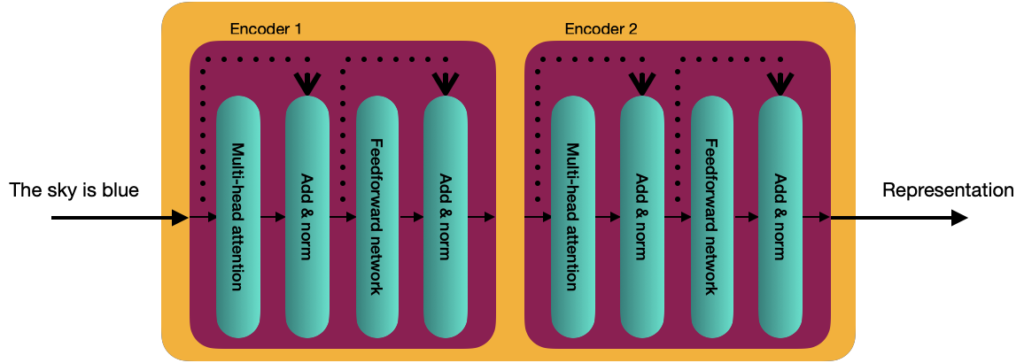
La normalización de capas permite un entrenamiento más rápido al evitar que los valores en cada capa cambien drásticamente.
El decodificador
De la misma manera que el codificador, podemos tener una pila de N decodificadores (por ejemplo, asumimos que N=2). La representación de la secuencia producida por los codificadores es la entrada de todos los decodificadores; es decir, un decodificador recibe dos entradas, una del decodificador anterior y la representación hecha por el codificador.
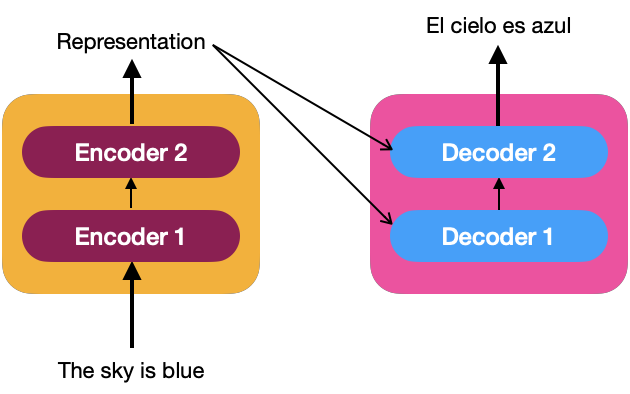
Para comprender cómo el decodificador genera la oración objetivo, echemos un vistazo a la siguiente imagen que describe la entrada al decodificador como una serie temporal.
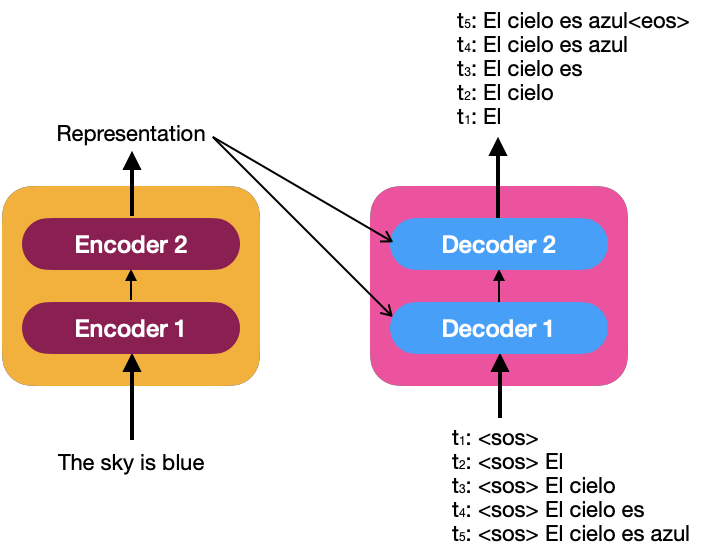
<eos>: End Of the Sentence
En cada paso de tiempo, el decodificador compara la palabra recién generada con la entrada y predice la siguiente entrada. Una vez que se genera el token <eos>, el decodificador ha terminado de generar la oración objetivo.
Al igual que el incrustado de entrada para los codificadores, la oración <sos>» El cielo es azul» debe ser incrustada para alimentar a los decodificadores.
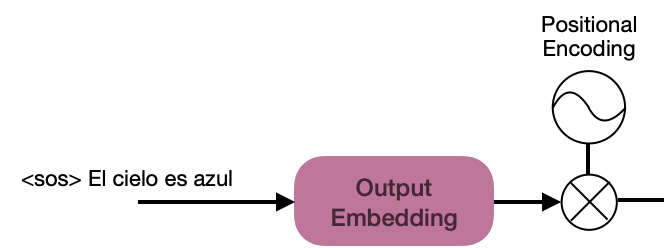
Para entender cómo funciona el decodificador, debes explorar sus componentes en la imagen a continuación:
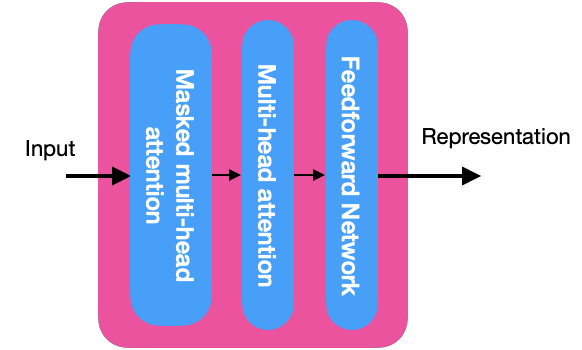
Atención Multicabezal Enmascarada
La atención multicabezal enmascarada es similar al mecanismo de atención multicabezal con una pequeña diferencia
Durante una prueba, el decodificador generará palabras siempre que haya un valor previo; es decir, para la entrada en «t2: <sos> El», el modelo se entrena solo con los tokens <sos> y El, y el mecanismo de atención debe coincidir con las palabras solo hasta la palabra El y no para las palabras faltantes en la oración. El resto de las palabras en la secuencia pueden ser enmascaradas, lo que ayuda al mecanismo de atención a prestar atención únicamente a las palabras disponibles durante las pruebas.
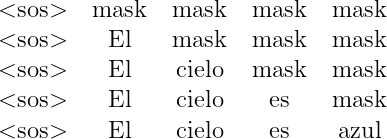
Debemos calcular la matriz de atención Z de la misma manera que lo hemos estado haciendo, con la diferencia de que los valores correspondientes a la palabra enmascarada de la oración reciben un valor de -\infty. Por ejemplo:
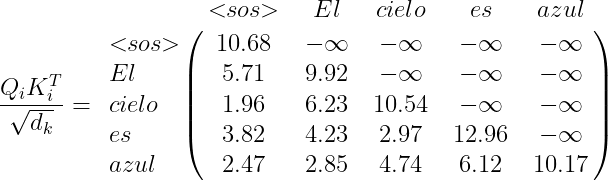
Con esto, podemos obtener la matriz de atención final como lo hicimos para el codificador, y esta matriz alimentará la siguiente capa de atención multicabezal.
Masked \; multihead \; attention=Concatenate\left ( Z_1, Z_2, Z_3, Z_4, Z_5, Z_6, Z_7, Z_8 \right ) \cdot W_0
Atención Multicabezal
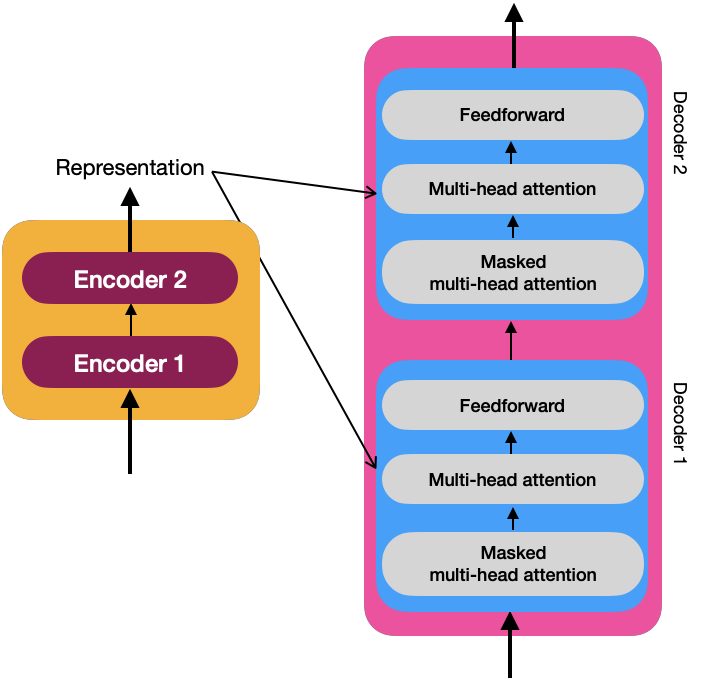
En la imagen anterior, puedes ver los detalles internos de los decodificadores, y cada capa de atención multicabezal recibe la representación R de la salida de los codificadores y la atención multicabezal enmascarada M de la capa anterior. Debido a la interacción de esta capa entre el decodificador y el codificador, también se llama atención codificador-decodificador.
Para calcular el mecanismo de atención, obtenemos la matriz de consulta Q utilizando la matriz M; y las matrices K y V utilizando la matriz R.
- Q_i = M \times W_i^Q
- K_i = R \times W_i^K
- V_i = R \times W_i^V
Q_i representa la oración objetivo obtenida de M, y las matrices K y V contienen la representación R obtenida de los codificadores.
A continuación se presenta el procedimiento para obtener la matriz de auto-atención:
Z_i=Softmax\left ( \frac{Q_iK_{i}^{T}}{\sqrt{d_k}} \right ) \cdot V_i
Al calcular el producto Q_iK_{i}^{T}, observaremos que el resultado contendrá una matriz que se aproxima a la matriz identidad, lo que nos ayuda a comprender cuán similar es Q (que representa la oración objetivo) a la matriz K (que representa la oración fuente). Por ejemplo:
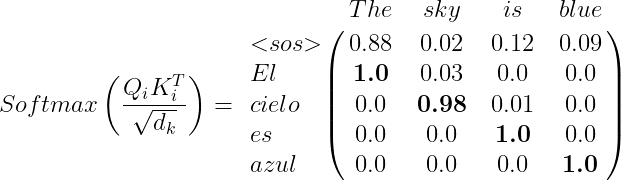
La matriz de atención se obtiene de la misma manera que en las secciones anteriores:
Multihead \; attention=Concatenate\left ( Z_1, Z_2, Z_3, Z_4, Z_5, Z_6, Z_7, Z_8 \right ) \cdot W_0
Red Prealimentada
Esta capa en el decodificador funciona de la misma manera que en el codificador. El componente de suma y normalización conecta las subcapas de entrada y salida, como se muestra en la siguiente imagen:
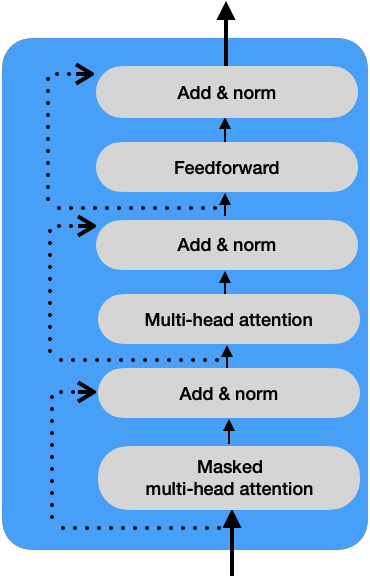
Capa Lineal y Capa Softmax
El decodificador aprende la representación de la oración objetivo, que será alimentada a las capas lineal y softmax.
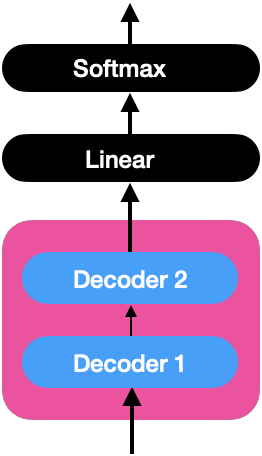
Capa Lineal
Esta capa genera los logits con el tamaño del vocabulario. Asumiendo que el vocabulario es:
Vocabulary=\left [ azul, cielo, El, es \right ]
Asumiendo que la entrada al decodificador es «El», el vector de logits generado por el decodificador, por ejemplo, sería:
logits=\left [ 40, 51, 43, 38 \right ]
Capa Softmax
Cuando aplicamos la función Softmax al vector de logits mencionado anteriormente, obtenemos un vector de probabilidades, por ejemplo:
prob=\left [ 0.005, 0.973, 0.015, 0.007 \right ]
La palabra del vocabulario con el valor de probabilidad más alto es «sky,» por lo que esta palabra es la siguiente predicción del decodificador.
Entrenamiento del Transformador
El objetivo del entrenamiento del modelo es minimizar la función de pérdida. Para el Transformador, tenamos que minimizar la diferencia entre las distribuciones de probabilidad y la predicha. La función de pérdida que mejor se adapta a este tipo de escenario es la «función de pérdida de entropía cruzada (cross-entropy)«, y usamos el optimizador Adam.
Para prevenir el sobreajuste, aplicamos dropout a la salida de cada subcapa y a la suma de los incrustados y la codificación posicional.
Conclusión
Los conceptos mostrados en esta publicación son esenciales para comprender el funcionamiento interno de los modelos actualmente bien conocidos, como GPT-3, BERT, y otros más modernos, como PaLM, entre otros. Comprenderlos nos ayudará a apreciar y aprovechar mejor los beneficios que estos modelos de Transformadores ofrecen para los modelos de procesamiento del lenguaje natural (NLP) al desarrollar soluciones creativas, como ChatGPT.
Si crees que este contenido es útil, considera comprarme un café. 😉☕️👉🏼