Actualización 09.2022
Esta entrada ha sido actualizada con la versión de TensorFlow v2.10.0 y PyTorch 1.12.1
Tabla de Contenidos
¿Qué es una función de activación?
Una función de activaciónes una función que se aplica a una neurona en una red neuronal para ayudarla a aprender patrones complejos de datos, decidiendo lo que debe ser transmitido a la siguiente neurona en la red.
Un perceptrón es una unidad de una red neuronal que ingresa los datos de los que se quiere aprender hacia una neurona, y los procesa de acuerdo a su función de activación.
El perceptrón es un algoritmo simple que, dado un vector de entrada x de m valores (x_1, x_2, ..., x_m), dá como salida un 1 o un 0 (función escalonada), y su función se define a continuación:
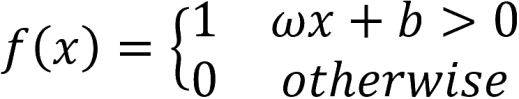
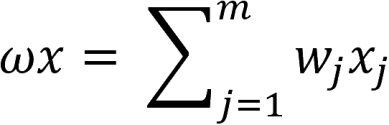
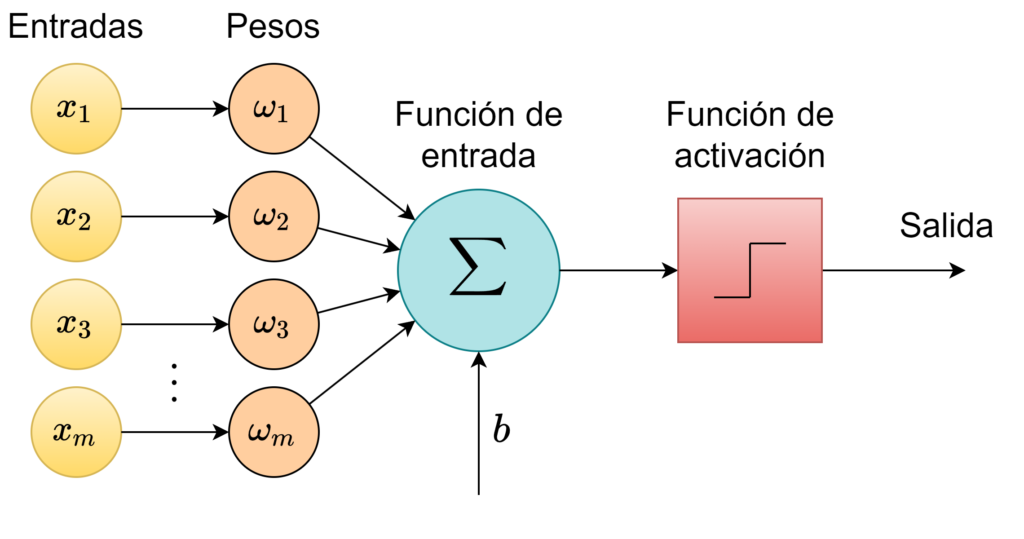
Aqui, ω es un vector de pesos, ωx es el producto punto, y b es el sesgo, o tendencia. Esta ecuación reensambla la ecuación de la recta. Si x se encuentra sobre esta línea, entonces la respuesta es positiva, de otro modo es negativa. Sin embargo, idealmente vamos a pasar datos de entrenamiento y permitir al computador ajustar el peso y el sesgo de tal manera que los errores producidos por esta neurona se minimicen. El proceso de aprendizaje debería ser capaz de reconocer pequeños cambios que progresivamente enseñan a nuestra neurona a clasificar la información como queremos.
La siguiente imagen es una función escalonada donde si x>0 la salida es 1, y si x<0 la salida es 0, como función de activación no nos sirve ya que no tenemos «pequeños cambios» sino un gran cambio, y la neurona no es capaz de aprender de esta manera ya que ω y b no van a converger a los valores óptimos para minimizar errores.
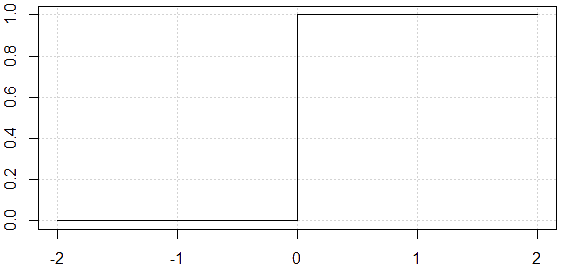
La tangente de la función de activación indica si la neurona está aprendiendo; de la imagen anterior deducimos que la tangente en x=0 es \infty. Esto no es posible en escenarios reales porque en la vida real todo lo aprendemos paso a paso. Para que una neurona aprenda, necesitamos algo que cambie progresivamente de 0 a 1, es decir, una función continua (y derivable).
Cuando comenzamos a usar redes neurales, usamos funciones de activación como parte esencial de una neurona. Esta función de activación nos permitirá ajustar pesos y sesgos.
La derivada de la función de activación alimenta el algoritmo de backpropagation durante el aprendizaje. Por esta razón es que la función y su derivada deben tener un costo computacional bajo
Funciones de Activación
Actualmente existen varios tipos de funciones de activacion que son utilizadas en varios escenarios. A contuación una explicación corta de las funciones de activación disponibles en el módulo tf.keras.activations de la distribución de TensorFlow v2.10.0 y torch.nn de PyTorch 1.12.1
Sigmoide
\sigma \left ( x \right )=\frac{1}{1+e^{-x}}
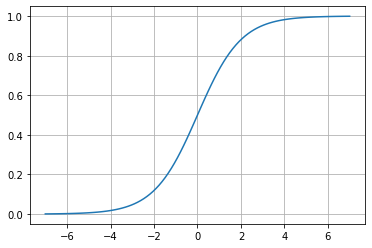
Matemáticamente, esta función es continua. Como podemos ver, en la sigmoide los cambios son graduales y podemos tener valores distintos de 0 o 1.
![]() Ejemplo:
Ejemplo:
import tensorflow as tf
import matplotlib.pyplot as plt
X = tf.linspace(-7., 7., 100)
y = tf.keras.activations.sigmoid(X)
plt.plot(X,y)
plt.grid()
![]() Ejemplo:
Ejemplo:
import torch
import matplotlib.pyplot as plt
X = torch.linspace(-7., 7., steps=100)
y = torch.nn.Sigmoid()(X)
plt.plot(X,y)
plt.grid()
Míralo en Google Colab aquí: Activation Functions
La función sigmoide es la función de activación más común; sin embargo, no se la utiliza frecuentemente debido a la tendencia a llevar los términos de backpropagation (no me suena bien «propagación hacia atrás», disculpen) a cero durante el entrenamiento.
ReLU (Rectified Linear Unit)
f(x)=max(0,x)
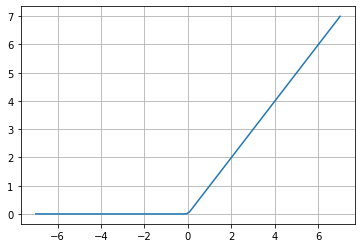
Esta función ha llegado a ser muy popular ya que genera muy buenos resultados experimentales. La mayor ventaja de ReLU es que esta función acelera la convergencia del Stochastic Gradient Descent (SGD), lo cual indica qué tan rápido está aprendiendo la neurona, comparádola con las funciones Sigmoide y Tangente Hiperbólica.
Sin embargo, esta fortaleza es, a su vez, su mayor debilidad puesto que esta «velocidad de aprendizaje» puede hacer que los pesos \omega de la neurona se actualicen y oscilen desde los valores óptimos y no se activen en ningún punto. Por ejemplo, si la taza de aprendizaje es demasiado alta, la mitad de las neuronas pueden estar «muertas», pero si se establece un valor apropiado entonces las neuronas aprenderán, pero será más lento que lo esperado.
![]() Ejemplo:
Ejemplo:
import tensorflow as tf
import matplotlib.pyplot as plt
X = tf.linspace(-7., 7., 100)
y = tf.keras.activations.relu(X)
plt.plot(X,y)
plt.grid()
![]() Ejemplo:
Ejemplo:
import torch
import matplotlib.pyplot as plt
X = torch.linspace(-7., 7., steps=100)
y = torch.nn.ReLU()(X)
plt.plot(X,y)
plt.grid()
Míralo en Google Colab aquí: Activation Functions
ReLU6
f(x)= min(max(0,x), 6)
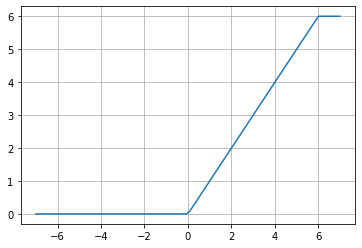
Esta función ha permanecido históricamente en el módulo tf.nn, heredada desde TensorFlow 1. Fue introducida en el paper «Convolutional Deep Belief Networks on CIFAR-10» (página 2), con la ventaja, comparándola con la ReLU simple, de que es computacionalmente más rápida y no sufre de valores que «explotan». Como podemos inferir a partir del paper que la introdujo, ha sido utilizada en redes neurales Convolucionales (CNN) y Recurrentes (RNN).
![]() Ejemplo:
Ejemplo:
import tensorflow as tf
import matplotlib.pyplot as plt
X = tf.linspace(-7., 7., 100)
y = tf.nn.relu6(X)
plt.plot(X,y)
plt.grid()
![]() Ejemplo:
Ejemplo:
import torch
import matplotlib.pyplot as plt
X = torch.linspace(-7., 7., steps=100)
y = torch.nn.ReLU6()(X)
plt.plot(X,y)
plt.grid()
Míralo en Google Colab aquí: Activation Functions
Tangente Hiperbólica
f(x)= tanh(x)
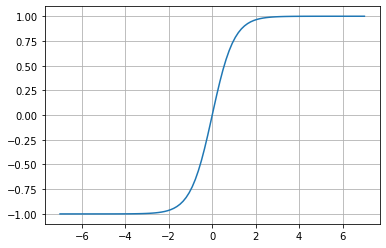
Esta función es muy similar a la sigmoide, excepto que en lugar de tener un rango entre 0 y 1, el rango es de -1 a 1. Tristemente, tiene el mismo problema de desvanecimiento de la sigmoide.
![]() Ejemplo:
Ejemplo:
import tensorflow as tf
import matplotlib.pyplot as plt
X = tf.linspace(-7., 7., 100)
y = tf.keras.activations.tanh(X)
plt.plot(X,y)
plt.grid()
![]() Ejemplo:
Ejemplo:
import torch
import matplotlib.pyplot as plt
X = torch.linspace(-7., 7., steps=100)
y = torch.nn.Tanh()(X)
plt.plot(X,y)
plt.grid()
Míralo en Google Colab aquí: Activation Functions
ELU (Exponential Linear Unit)
Dado un valor de \alpha>0
f(x)=x\;\;if\;\;x\geq 0
f(x)=\alpha (e^{x}-1)\;\;if\;\;x<0
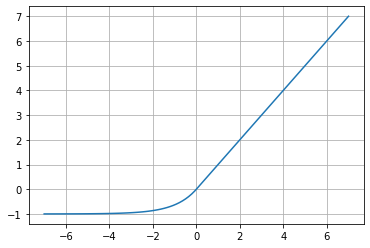
De acuerdo al paper «Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)«, esta función tiende a convergir a cero más rápido y produce resultados más exactos. Su comportamiento es similar a ReLU, pero para valores negativos donde exponencialmente tiende a -\alpha.
Es una función común en CNN, como lo indica su paper de investigación.
![]() Ejemplo:
Ejemplo:
import tensorflow as tf
import matplotlib.pyplot as plt
X = tf.linspace(-7., 7., 100)
y = tf.keras.activations.elu(X, alpha=1.0)
plt.plot(X,y)
plt.grid()
![]() Ejemplo:
Ejemplo:
import torch
import matplotlib.pyplot as plt
X = torch.linspace(-7., 7., steps=100)
y = torch.nn.ELU()(X)
plt.plot(X,y)
plt.grid()
Míralo en Google Colab aquí: Activation Functions
Softmax
Dado un vector de valores x, y un número de clases K de un clasificador multi-clases:
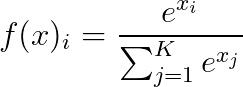
Softmax comvierte un vector de valores a una distribución de probabilidad de suma 1, como podemos ver, su utilización difiere del resto de funciones de activación en que esta función se la utiliza como la capa final en clasificadores basados en redes neurales.
Esta función no es únicamente utilizada en clasificadores, sino también en el aprendizaje reforzado para convertir valores en probabilidades de actuación. Como indica Wikipedia:
Correlaciona la recompensa que se espera obtener al llevar a cabo una acción específica con la probabilidad de escoger esa acción. De este modo las acciones de mayor recompensa esperada se eligen con mayor probabilidad.
Wikipedia: Función Softmax
![]() Ejemplo:
Ejemplo:
import tensorflow as tf
inputs = tf.random.normal(shape=(32, 10))
outputs = tf.keras.activations.softmax(inputs)
tf.reduce_sum(outputs[0, :]) # Each sample in the batch now sums to 1
![]() Ejemplo:
Ejemplo:
import torch
inputs = torch.randn(32, 10)
outputs = torch.nn.Softmax(dim=1)(inputs)
torch.sum(outputs[0, :]) # Each sample in the batch now sums to 1
Míralo en Google Colab aquí: Activation Functions
Softplus
f(x)=ln(1+e^{x})
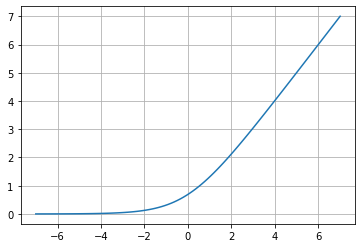
Esta función es una alternativa a las funciones tradicionales, como la Sigmoide o la Tangente Hiperbólica, debido a que es derivable (lo cual es importante para la función de backpropagation). Lo sorprendente con la derivada de esta función es que ¡es la función Sigmoide!
\frac{\partial y}{\partial x}=\left ( ln(1+e^x) \right )'=\left ( \frac{1}{1+e^x} \right )\left ( 1+e^x \right )'
\frac{\partial y}{\partial x}=\left ( \frac{1}{1+e^x} \right )\cdot e^x=\frac{e^x}{1+e^x}=\frac{e^{x}}{e^{x}\left ( e^{-x}+1 \right )}
\therefore\;\; \frac{\partial y}{\partial x}=\frac{1}{1+e^{-x}}
Esto es interesante ya que nos permite entender con más claridad cómo se va a comportar el proceso de backpropagation.
![]() Ejemplo:
Ejemplo:
import tensorflow as tf
import matplotlib.pyplot as plt
X = tf.linspace(-7., 7., 100)
y = tf.keras.activations.softplus(X)
plt.plot(X,y)
plt.grid()
![]() Ejemplo:
Ejemplo:
import torch
import matplotlib.pyplot as plt
X = torch.linspace(-7., 7., steps=100)
y = torch.nn.Softplus()(X)
plt.plot(X,y)
plt.grid()
Míralo en Google Colab aquí: Activation Functions
Softsign
f(x)=\frac{x}{\left ( 1+\left | x \right | \right )}
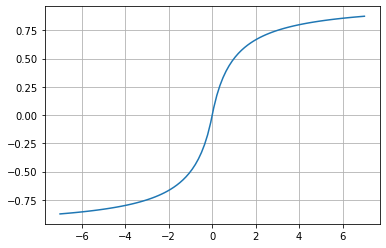
Dada la forma de la gráfica, podemos ver que es una alternativa a la Tangente Hiperbólica pero no ha sido tan ampliamente adoptada; sin embargo, considerando que la función de activación es un estado-del-arte, podría ser la función que mejor se adapte a determinados modelos de redes neurales.
![]() Ejemplo:
Ejemplo:
import tensorflow as tf
import matplotlib.pyplot as plt
X = tf.linspace(-7., 7., 100)
y = tf.keras.activations.softsign(X)
plt.plot(X,y)
plt.grid()
![]() Ejemplo:
Ejemplo:
import torch
import matplotlib.pyplot as plt
X = torch.linspace(-7., 7., steps=100)
y = torch.nn.Softsign()(X)
plt.plot(X,y)
plt.grid()
Míralo en Google Colab aquí: Activation Functions
Swish
f(x)=\frac{x}{1+e^{-x}}
f(x)=x\cdot Sigmoid(x)
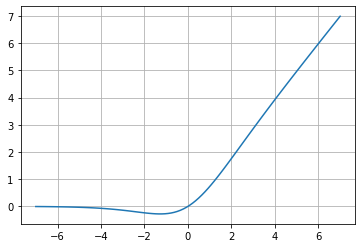
Esta función de activación es relativamente nueva (2017), y supera a ReLU para redes CNN más profundas. La ecuación que define esta función describe una Sigmoid(x), pero no tiene el problema de desvanecimiento del gradiente, el factor x hace que esta función sea importante nuevamente.
Con respecto a su comparativa con ReLU, ReLU tenía el problema de producir salida 0 para valores negativos que no pueden añadirse a backpropagation, Swish maneja este problema parcialmente; sin embargo, el costo computacional de Swish es mayor y es un tema que debe evaluarse para su decisión ya que este costo será llevado al proceso de backpropagation.
![]() Ejemplo:
Ejemplo:
import tensorflow as tf
import matplotlib.pyplot as plt
X = tf.linspace(-7., 7., 100)
y = tf.keras.activations.swish(X)
plt.plot(X,y)
plt.grid()
![]() Ejemplo:
Ejemplo:
import torch
import matplotlib.pyplot as plt
# It's interesting that PyTorch doesn't have a built-in swish function
X = torch.linspace(-7., 7., steps=100)
y = X * torch.nn.Sigmoid()(X)
plt.plot(X,y)
plt.grid()
Míralo en Google Colab aquí: Activation Functions
Sinc
f(x)=\frac{sin(x)}{x}\;\;if\;\;x\neq 0
f(x)=1\;\;if\;\;x=0
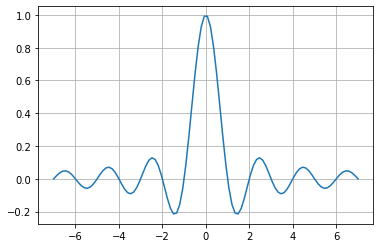
Sinc es una función de activación fuera de lo común ya que, en contraste con las otras funciones, esta sube y cae. Sin embargo, la función se satura y su salida converge a cero para valores de entrada positivos y negativos grandes.
La función tiene una excepción en x=0 ya que si se evalúa ese valor en f(x)=\frac{sin(x)}{x} se obtendría una ideterminación de divisón por 0.
Las funciones periódicas como Sinc no son populares en redes neurales como funciones de activación. Pero aún cuando sinc es periódica, se saturará cuando el valor de entrada incremente positiva o negativamente, tal como otras funciones como la Sigmoide o la Tangente Hiperbólica, lo cuando hace a esta función una alternativa interesante como función de activación en redes neurales.
![]() Ejemplo:
Ejemplo:
import tensorflow as tf
import matplotlib.pyplot as plt
X = tf.linspace(-7., 7., 100)
y = tf.experimental.numpy.sinc(X)
plt.plot(X,y)
plt.grid()
![]() Ejemplo:
Ejemplo:
import torch
import matplotlib.pyplot as plt
X = torch.linspace(-7., 7., steps=100)
y = torch.special.sinc(X)
plt.plot(X,y)
plt.grid()
Míralo en Google Colab aquí: Activation Functions
Leaky ReLU
Dado un valor de \alpha>0
f(x)=x\;\;if\;\;x\geq 0
f(x)=\alpha x\;\;if\;\;x<0
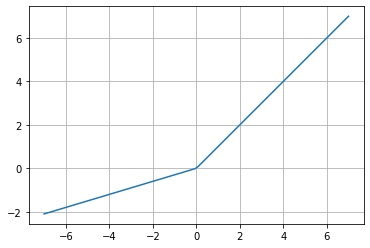
ReLU es una función de activación muy popular en CNN, ya que para valores positivos no llega a saturarse y detener el aprendizaje; sin embargo, una debilidad de la ReLU es que para valores negativos tiende a saturarse, y Leaky ReLU (LReLU) corrije este problema.
TensorFlow establece un valor default para la constante \alpha=0.3, aunque algunas fuentes mencionan un valor de 0.01. En términos generales, \alpha establece la pendiente de la ecuación para valores negativos, y LReLU mejora la el rendimiento de la convergencia.
![]() Ejemplo:
Ejemplo:
import tensorflow as tf
import matplotlib.pyplot as plt
X = tf.linspace(-7., 7., 100)
leakyReLU = tf.keras.layers.LeakyReLU(alpha=0.3)
y = leakyReLU(X)
plt.plot(X,y)
plt.grid()
![]() Ejemplo:
Ejemplo:
import torch
import matplotlib.pyplot as plt
X = torch.linspace(-7., 7., steps=100)
y = torch.nn.LeakyReLU(0.3)(X)
plt.plot(X,y)
plt.grid()
Míralo en Google Colab aquí: Activation Functions
Mish
f(x)=x\cdot tanh(softplus(x))
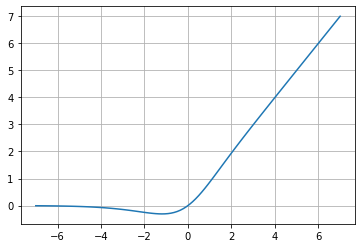
Por su forma, esta función es muy similar a Swish, definida como «una función de activación no-monotónica auto-regulada«, según su paper de investigación (2020). La parte innovadora de Mish es dada por la comprensión intuitiva del comportamiento de la derivada, para entender cómo ayuda a regularizar la optimización de las redes neurales.
\frac{\partial y}{\partial x}=(x\cdot tanh(softplus(x)))'=(x\cdot tanh(1+e^{x}))'
\frac{\partial y}{\partial x}=\frac{e^{x}\omega }{\delta ^{2}}
Donde:
\omega =4(x+1)+4e^{2x}+e^{3x}+e^{x}(4x+6)
\delta =2e^{x}+e^{2x}+2
Estas funciones son más sencillas de graficar y darnos una mejor comprensión de cómo se va a comportar el proceso de backpropagation.
![]() Ejemplo:
Ejemplo:
! pip install tensorflow-addons
import tensorflow as tf
import tensorflow_addons as tfa
import matplotlib.pyplot as plt
X = tf.linspace(-7., 7., 100)
y = tfa.activations.mish(X)
plt.plot(X,y)
plt.grid()
![]() Ejemplo:
Ejemplo:
import torch
import matplotlib.pyplot as plt
X = torch.linspace(-7., 7., steps=100)
y = torch.nn.Mish()(X)
plt.plot(X,y)
plt.grid()
Míralo en Google Colab aquí: Activation Functions
GELU (Gaussian Error Linear Unit)
f(x)=xP(X\leq x)=x\;\Phi (x)=x\cdot \frac{1}{2}\left [ 1+erf(\frac{x}{\sqrt{2}}) \right ]
f(x)\approx 0.5x\left ( 1+tanh\left [ \frac{\sqrt{2}}{\pi}\left ( x+0.044715x^{3} \right ) \right ] \right )
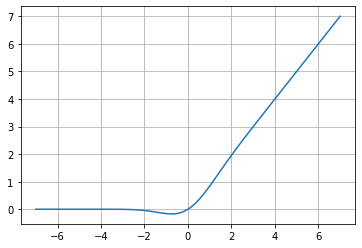
Esta función pretende fusionar la funcionalidad de una Unidad Linear (ReLU, ELU) con la función de regularización Dropout, por medio de una multiplicación estocástica del vector de entrada por 0 o por 1, y obtener la función de activación de manera determinista.
GELU, como está determinada en su paper de investigación, está determinada por una función de distribución Gaussiana lo cual elimina el problema de desvanecimiento en valores negativos que tiene ReLU, mejorando su rendimiento para tareas como computer vision, NLP y procesamiento de voz.
![]() Ejemplo:
Ejemplo:
import tensorflow as tf
import matplotlib.pyplot as plt
X = tf.linspace(-7., 7., 100)
y = tf.keras.activations.gelu(X)
plt.plot(X,y)
plt.grid()
![]() Ejemplo:
Ejemplo:
import torch
import matplotlib.pyplot as plt
X = torch.linspace(-7., 7., steps=100)
y = torch.nn.GELU()(X)
plt.plot(X,y)
plt.grid()
Míralo en Google Colab aquí: Activation Functions
SELU (Scaled Exponential Linear Unit)
f(x)=\lambda x\;\;if\;\;x\geq 0
f(x)=\lambda \alpha (e^{x}-1)\;\;if\;\;x<0
Donde \alpha \approx 1.6733 y \lambda \approx 1.0507
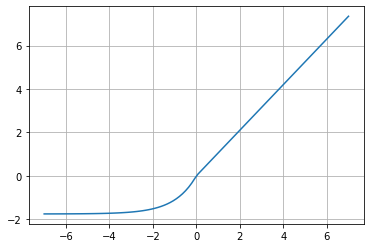
SELU es una función de activación que induce propiedades de auto-normalización que converge a una media cero y varianza unitaria. A diferencia de ReLU, puede alcanzar valores bajo 0, lo que permite a la red neural tener una salida de media 0, y esta característica ayuda al modelo a converger más rápidamente hacia la solución.
![]() Ejemplo:
Ejemplo:
import tensorflow as tf
import matplotlib.pyplot as plt
X = tf.linspace(-7., 7., 100)
y = tf.keras.activations.selu(X)
plt.plot(X,y)
plt.grid()
![]() Ejemplo:
Ejemplo:
import torch
import matplotlib.pyplot as plt
X = torch.linspace(-7., 7., steps=100)
y = torch.nn.SELU()(X)
plt.plot(X,y)
plt.grid()
Míralo en Google Colab aquí: Activation Functions